How to use Eigen Geometry library for c++

The Eigen Geometry library is a C++ libary useful for robotics. It is capable of the following operations:

  1. Declare Vectors, matrices, quaternions.
    • Perform operations like dot product, cross product, vector/matrix addition ,subtraction, multiplication.
    • Convert from one form to another. For instance one can convert quaternion to affine pose matrix and vice versa.
    • Use AngleAxis function to create rotation matrix in a single line.

Example Implementation

To use the library, the following includes are recommended:

#include <Eigen/Geometry>
#include <Eigen/Dense>
#include <eigen_conversions/eigen_msg.h>
#include <Eigen/Core>

For instance, a rotation matrix homogeneous transform of PI/2 about z-axis can be written as:

Eigen::Affine3d T_rt(Eigen::AngleAxisd(M_PI/2.0, Eigen::Vector3d::UnitZ()));

Additionally, you can:

  1. Extract rotation matrix from Affine matrix using Eigen::Affine3d Mat.rotation( )
    • Extract translation vector from Affine Matrix using Eigen::Affine3d Mat.translation( )
    • Find inverse and transpose of a matrix using Mat.inverse( ) and Mat.transpose( )

The applications are the following

  1. Convert Pose to Quaternions and vice versa
  2. Find the relative pose transformations by just using simple 3D homogeneous transformation Eigen::Affine3d T is a 4*4 homogeneous transform: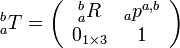 Homogeneous Equation Example
  3. Now all the transformations (rotation or translation) can be represented in homogeneous form as simple 4*4 matrix multiplications.
  4. Suppose you have a pose transform T of robot in the world and you want to find robot’s X-direction relative to the world. You can do this by using Eigen::Vector3d x_bearing= T.rotation * Eigen::Vector3d::UnitX();

References

This is an important library in c++ which gives capabilities equal to Python for vectors and matrices. More helpful functions and examples can be found at the following links

  • Eigen Documentation: http://eigen.tuxfamily.org/dox/
  • Eigen Quaternion Documentation: https://eigen.tuxfamily.org/dox/classEigen_1_1Quaternion.html
  • Eigen Transforms Documentation: https://eigen.tuxfamily.org/dox/classEigen_1_1Transform.html